【数学編】中央大学の入試対策・オススメ参考書
更新日: (公開日: ) CHUO

本記事では中央大学の数学、その傾向と対策、勉強計画を紹介します。
・「MARCH」の「C」が中央大学
・全8学部
・偏差値55.0~65.0
関連:中央大学の偏差値・合格最低点ランキングはこちら!
各学部の入試傾向・対策
各学部の入試方式(商学部は会計学科/商業・貿易学科と経営学科/金融学科に分かれている)+全学部統一方式(文系)+センター利用方式(理系)
法学部
・試験時間:60分
・配点 :100点満点
・目標点 :80点
・問題数 :9問
・形式 :記述式
・構成 :大問3題
| 出題形式 | 問題数 | 配点 | 時間 | |
| 大問1 | 数列 | 3問 | 30点 | 15分 |
| 大問2 | 2次関数(うち1題はグラフ) | 3問 | 30点 | 20分 |
| 大問3 | 微分法(数学Ⅱまで) 数列 |
3問 | 40点 | 25分 |
| 計 | 9問 | 60分 |
・証明問題がよく出題される。
・レベルは標準的なものが多い。
・2019年度はグラフを書く問題が出題された。
・合格最低点が非常に高くなっている。
文学部
・試験時間:60分
・配点 :100点満点
・目標点 :75点
・問題数 :12問
・形式 :記述式
・構成 :大問3題
| 出題形式 | 問題数 | 配点 | 時間 | |
| 大問1 | 図形と方程式 | 5問 | 35点 | 15分 |
| 大問2 | 整数、帰納法 (うち1題は証明問題) |
3問 | 30点 | 20分 |
| 大問3 | 円と直線・領域 | 4問 | 35点 | 25分 |
| 計 | 12問 | 60分 |
・出題は基本~標準的な問題のものからが多い。
・2019年度は帰納法の証明問題が出題された。
・例年、求積問題が出題されている。
経済学部
・試験時間:60分
・配点 :100点満点
・目標点 :80点
・問題数 :問
・形式 :記述式
・構成 :大問3題
| 出題形式 | 問題数 | 配点 | 時間 | |
| 大問1 | 小問集合 (整数・不等式・ベクトル・場合の数・微分・積分) |
6問 | 36点 | 20分 |
| 大問2 | 三角関数 | 3問 | 32点 | 20分 |
| 大問3 | 数列 | 3問 | 32点 | 20分 |
| 計 | 12問 | 60分 |
・第1問の小問集合に関して、幅広い分野から出題される。
・レベルは標準的なものが多い。
・2019年度はグラフや証明問題などの記述問題は出題されなかった。
・第1問の答えは結果のみを記述する。
商学部(会計学科/商業・貿易学科)
・試験時間:60分
・配点 :100点満点
・目標点 :75点
・問題数 :7問
・形式 :記述式
・構成 :大問4題
| 出題形式 | 問題数 | 配点 | 時間 | |
| 大問1 | 整数 | 2問 | 25点 | 20分 |
| 大問2 | ベクトル | 2問 | 25点 | 13分 |
| 大問3 | 不等式 | 1問 | 25点 | 12分 |
| 大問4 | 確率 | 2問 | 25点 | 15分 |
| 計 | 7問 | 60分 |
・出題は基本~標準的な問題のものからが多い。
・2019年度は長い記述を求める問題は出題されなかった。
・他の文系学部と違い、大問が4題に分かれている。
商学部(経営学科/金融学科)
・試験時間:60分
・配点 :100点満点
・目標点 :75点
・問題数 :7問
・形式 :記述式
・構成 :大問4題
| 出題形式 | 問題数 | 配点 | 時間 | |
| 大問1 | 不等式 | 2問 | 25点 | 20分 |
| 大問2 | 数列 | 2問 | 25点 | 15分 |
| 大問3 | 図形と方程式 | 1問 | 25点 | 10分 |
| 大問4 | 確率 | 2問 | 25点 | 15分 |
| 計 | 7問 | 60分 |
・出題は基本的な問題が多い。
・2019年度は長い記述を求める問題は出題されなかった。
・他の文系学部と違い、大問が4題に分かれている。
・商学部は共通して確率に分野が毎年出題されている。
全学部
・試験時間:60分
・配点 :100点満点
・目標点 :75点
・問題数 :12問
・形式 :記述式
・構成 :大問4題
| 出題形式 | 問題数 | 配点 | 時間 | |
| 大問1 | 集合 | 3問 | 20点 | 15分 |
| 大問2 | 図形と方程式 | 3問 | 20点 | 15分 |
| 大問3 | 微分法・積分法 | 3問 | 30点 | 15分 |
| 大問4 | 確率 | 3問 | 30点 | 15分 |
| 計 | 12問 | 60分 |
・集合や確率など、数学Ⅰの分野からの出題が比較的多い。
・問題のレベルは標準的なものが多い。
・第3問では、実際にグラフを描く問題が出題された。
・他の文系学部と違い、大問が4題に分かれている。
理工学部
・試験時間:100分
・配点 :100点満点
・目標点 :80点
・問題数 :20問
・形式 :記述式、マーク式
・構成 :大問4題
| 出題形式 | 問題数 | 配点 | 時間 | |
| 大問1 | 複素数平面 | 4問 | 15点 | 20分 |
| 大問2 | 積分法 | 8問 | 25点 | 25分 |
| 大問3 | 確率 | 4問 | 30点 | 25分 |
| 大問4 | 積分法 | 4問 | 30点 | 30分 |
| 計 | 20問 | 100分 |
・積分法などの数学Ⅲの範囲からの出題が多い。
・問題のレベルは標準的なものが多い。
・数学Ⅲの範囲からの出題が多いことにより、計算量が多くなっている。
・マーク式と記述式が併用されている。
・大問1,2においてマーク式での回答が求められるが、センター試験とは違い選択肢が与えられている。
センター試験利用(併用)方式
・試験時間:100分
・配点 :100点満点
・目標点 :80点
・問題数 :20問
・形式 :記述式、マーク式
・構成 :大問4題
| 出題形式 | 問題数 | 配点 | 時間 | |
| 大問1 | 多項式 | 4問 | 50点 | 25分 |
| 大問2 | 極限 | 3問 | 50点 | 25分 |
| 大問3 | 複素数と方程式 | 3問 | 50点 | 25分 |
| 大問4 | 積分法 | 3問 | 50点 | 25分 |
| 計 | 20問 | 100分 |
・数学Ⅲの範囲からの出題が多い。
・数学Ⅲの範囲からの出題が多いことにより、計算量が多くなっている。
・2019年度は、証明問題が6題出題された。
・証明問題が他の入試方式よりも多く出題されるため、時間配分に注意する必要がある。
数学オススメ参考書

「初めから始める数学」の使い方はコチラ!
<特徴>
同目的の他の参考書と比べて解説量が2倍以上あることや噛み砕いて丁寧に説明されていることなどから数学に対して苦手意識を持っている人や高校数学初学者にも分かりやすい参考書となっています。説明文が話し口調で書かれているため親しみやすいという点も大きな特徴の1つです。
この参考書は問題集ではないため問題数が多くはありません。そのため、解き方のパターンをインプットした後は(または並行して)問題集に取り組むことをおすすめします。
<使用時期>
高校数学・学校の教科書や授業内容が全く理解できない状態で受験勉強を始めるのであれば、受験勉強開始と同時にこのシリーズの数学Ⅰに取り組みましょう。2月から受験勉強を始める場合は、2月に数学Ⅰ、3月に数学Aといったように1か月に1冊を完成させるイメージで進めていけば5か月で終わらせることができます。
教科書やそれに準ずる参考書を使って入試基礎レベルの知識やテクニックをインプットしたあとは「基礎問題精講」シリーズを使って、問題に当たるときに即座に解法を思いだすための訓練を行いましょう。


「数学 基礎問題精講」の使い方はコチラ!
<特徴>
例題・精講・解答解説・演習問題が見開き1ページに掲載されている、非常に見やすいレイアウトが特徴の参考書です。精講とはその例題を解く際に必要な公式などが説明されている部分のことです。
この部分を深く読み込んで理解することで他の問題に応用するための力を身につけることができます。ただし、演習問題の解説が十分ではないといった欠点があるため、理解が不十分でないと感じた部分に関しては教科書や前出の「初めから始める数学」シリーズなどに戻って理解の穴を作らないようにしましょう。
<使用時期>
前述したように解説が十分ではない部分があるため、高校数学初学者に適した参考書であるとは言い難いものとなっています。そのため、この参考書の中で不明点が出てきた場合は前出の「初めから始める数学」シリーズや学校の参考書などの該当箇所を参考にして、疑問点をそのままにしないようにしましょう。
具体的な使用時期としては5月から7月の3か月で3冊を完成させることをおすすめします。
「センター試験過去問研究数学」
<特徴>
過去実際にセンター試験で出題された問題と解答・解説が掲載されています。数学ⅠA・数学ⅡB全て合わせて54回分という豊富な問題量も大きな特徴の1つです。
比較的ていねいな解説が掲載されていますが万が一理解できない部分がある場合は前出の解説系参考書や学校の教科書などに戻って細かい部分まで確認するようにしましょう。
<使用時期>
基本的な解法技術や公式などを演習を通して理解し、問題を読んでから解答に取り掛かるスピードを上げるために使用します。
具体的な使用時期としては、前出の基礎問題精講を終えた8月に1か月かけて取り組むことが理想的です。以上がマークシート方式の典型的な形式である誘導のある問題に対応するための具体的な対策となります。
「合格る計算-数学Ⅲ-」の使い方はコチラ!
<特徴>
解説が非常に充実していることが大きな特徴の1つで受験生がやりがちな遠回りをすることになる計算方法を的確に提示したうえでそれよりも簡潔に短時間で計算できる方法を説明しています。
年度によって変動する可能性がありますが、マークシート方式で出題される場合、1つのケアレスミスが命取りとなってしまいます。
数学Ⅲはパターン問題を理解し暗記するだけで攻略できると言われており、その中で計算方法に関しても暗記すれば正解にたどり着けるものが多く存在します。前出の解説系参考書や学校の教科書などで土台となる知識を身に着けてからこの参考書を用いて計算方法のパターンも暗記してなるべく短い時間で正確に解答できるようにしましょう。
<使用時期>
前述したように、解説系参考書や教科書などで土台を固めてから取り組むことをおすすめします。
具体的な使用時期としては9月から10月の2か月間で、本番でも戦える計算の正確性とスピードを身につけることが理想的です。
まとめ
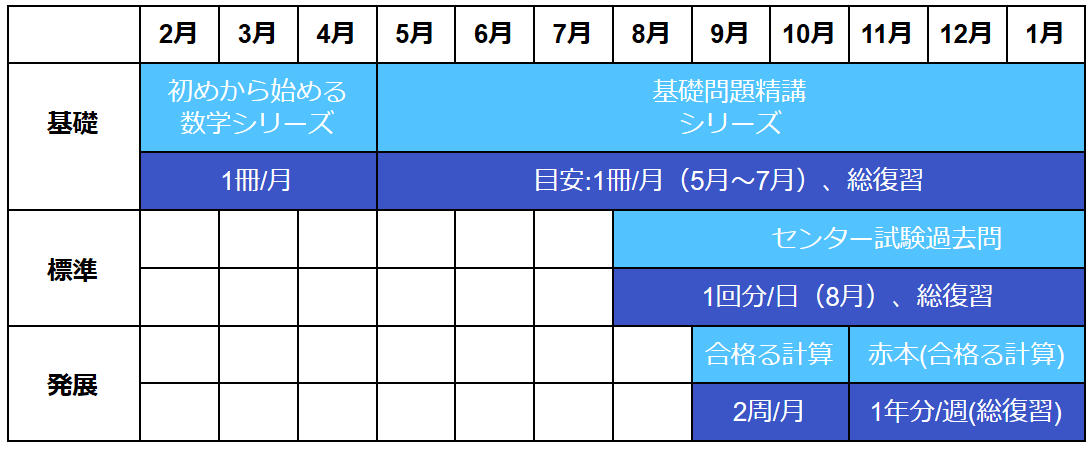 ※2月から受験勉強を始めた際の年間学習スケジュール
※2月から受験勉強を始めた際の年間学習スケジュール
まず始めるべきは数学Ⅰ・Ⅱ・Ⅲ・A・Bの基本的な問題の解き方のパターンのインプットです。教科書やそれに準ずる参考書を用いて,理解に穴を作らないようにしましょう。いずれも1度で終わらせず、何度も復習することが最も大切です。
その後、それぞれの演習系の参考書を用いて何度も実戦演習をし、秋以降はスムーズに赤本の演習に取り組んでいけるようにしましょう。
また、先の参考書で疑問点などが生じた場合は解説を読んで「分かった気」になるのではなく前のレベルの講義系参考書や教科書などに戻って公式などの再理解をすることも大切です。
合格するために重要なことは志望校の特徴にあった勉強を迷いなくすることです!マナビズムでは、自学自習で「何を勉強すればいいのか」「どうやって勉強すればいいのか」を教える「無料受験相談」を実施しています。
「中央大学に受かるために何からすればいいか不安!」「受験勉強を始めてみたものの成績が伸びずに不安!」といった人は、ぜひ無料受験相談をお申し込み下さい。









