【数学編】青山学院大学の入試対策・オススメ参考書

本記事では青山学院大学の理系数学の傾向と対策、合格するための勉強法について紹介します。青山学院大学は東京都渋谷区渋谷に本部を置く日本の私立大学です。キャンパスは2つあります。

1. 青山キャンパス （東京都渋谷区渋谷）
2. 相模原キャンパス（神奈川県相模原市中央区淵野辺）

16学部25学科が設置されており、2万人近くの学生が学ぶマンモス校となっています。首都圏の主な難関私立大学を指すMARCHの『A』の部分を占めている大学です。偏差値としては55.0～67.5で、就職・進路決定率は92.8％(2018年度)となっています。
青山学院大学の偏差値・合格最低点に関する詳細はコチラ！

はじめに

青山学院大学の入試の中で数学Ⅲの範囲を含む理系数学を採用している学部は理工学部のみです。出題形式はどの入試日程も同じであるため過去問演習の際はさまざまな入試形式・古い年度のものも使用し、演習慣れをすることをオススメします。

入試概要

• 試験時間：100分
• 配　　点：150点～200点（学科による）
• 目標点　：7～8割
• 問題数　：約35問（マークシート方式の空欄数と記述式の小問数の合計）
• 形　　式：マークシート方式・記述方式
• 構　　成：大問5題

大問［１］おもに数学ⅠAからの出題
大問［２］おもに数学ⅠA・ⅡB・Ⅲからの出題
大問［３］おもに数学ⅡB・Ⅲからの出題
大問［４］おもに数学ⅡB・Ⅲからの出題
大問［５］おもに数学Ⅲからの出題

傾向と対策

それでは今から青山学院大学の理系数学の大問毎の傾向と対策について紹介していきます。

大問［１］について

大問［１］の出題傾向として、数学ⅠAからの出題が多くなっていることがあげられます。

具体的には以下が挙げられます

• 数と式（2017年）
• 場合の数と確率（2018、2019年）

難易度は標準よりもやや易しいとされています。これらの範囲に関しては、学校の教科書と並行して「チャート式解法と演習数学IA(通称：黄チャート)」に取り組み、入試基礎レベルの完成に努めましょう。

「チャート式数学ⅠA」の使い方！
＜特徴＞
黄チャートは、日東駒専や産近甲龍などの中堅私立大学からMARCHや関関同立などの難関私立大学文系と国公立大学文系レベルをカバーしている参考書です。そのため、教科書や定期試験レベルの問題から入試の基礎レベルへの橋渡しとなる役割を果たすことが期待されます。

例題と解説、重要な公式やチェックポイントが1ページにまとめられた見やすいレイアウトと数学ⅠAの場合、837題という圧倒的な問題数が大きな特徴です。

＜使用時期＞
前述したように学校の定期試験から日東駒専や産近甲龍などといった中堅私立大学レベルへ引き上げるための参考書となっているため学校で配られる教科書などを利用し解法や公式を「覚えた」だけではなく「理解した」状態にしてからこの参考書に取り組むことが理想的です。

具体的な使用時期としては、受験勉強を2月に開始すると仮定すると2月～3月の2か月
最低3週以上取り組むことで理解の穴がない状態をつくることが望ましいです。この参考書が完璧に理解できるようになったら、「数学I・A-基礎問題精講-」に取り組み、青山学院大学理系数学の入試で戦えるレベルまで引き上げましょう。

「数学 基礎問題精講」の使い方！
＜特徴＞
例題・精講・解答解説・演習問題が見開き1ページに掲載されている、黄チャートと同様に見やすいレイアウトが特徴の参考書です。精講とは、例題を解く際に必要な公式などが詳しくポイントをまとめて説明されている部分のことです。
精講の部分を深く理解することで、他の問題にも応用できる本質を見抜く力を身につけることができます。ただし、演習問題の解説が十分ではないといった欠点があるため理解が不十分でないと感じた部分に関しては教科書や前出の黄チャートなどに戻って公式や解き方のパターンをもう一度確認するようにしましょう。

＜使用時期＞
前述したように解説が十分ではない部分があるため、高校数学初学者に適した参考書であるとは言い難いです。そのため、この参考書の中で少しでも不明点が出てきた場合は前出の黄チャートや学校の参考書などを利用して、理解に抜けがないようにしましょう。
具体的な使用時期としては4月の1か月に1冊を完成させることが理想的であるといえます。以上が大問［１］の数学ⅠAに対する具体的な対策になります。

大問［２］について

大問［２］はⅠA・ⅡB・Ⅲと年度によって出題範囲が違っていることが特徴の1つです。

• 2017年は場合の数と確率（数学A）
• 2018年は微分法（数学Ⅲ）
• 2019年は平面ベクトル（数学B）

難易度は大問［１］と同様に標準よりもやや易しいとされています。
この大問［２］で得点を重ねるためには、数学の全範囲の中で苦手分野を作ることなく、まんべんなく解答できるようにすることが重要です。数学ⅠA対策は大問［１］で述べてあるので、ここでは数学ⅡBの対策について説明していきます。
まず、数学ⅠAと同様に学校の教科書レベルから入試基礎レベルまで引き上げるために「チャート式解法と演習数学2-B（通称：黄チャート）」に取り組みましょう。

「チャート式数学ⅡB」の使い方！
＜特徴＞
先述したとおりです。数学ⅡBの場合、1160題という圧倒的な問題数が大きな特徴です。

＜使用時期＞
先述したとおりです。
具体的な使用時期としては、5月～6月の2か月間をかけて何周も取り組むことで自分の苦手分野を知りそこを重点的に演習するための準備ができている状態にしておくことが望ましいです。黄チャートで自分の苦手分野を把握したあとは「数学II・B-基礎問題精講-」を用いて入試基礎レベルを青山学院大学理系数学レベルまで引き上げましょう。

「数学 基礎問題精講」の使い方！
＜特徴＞
先述したとおりです。

＜使用時期＞
前述したように解説が十分ではない部分があるため、高校数学初学者にはあまりおすすめできません。そのため、この参考書の中で少しでも不明点が出てきた場合は前出の黄チャートや学校の参考書などを利用して、理解に抜けがないようにしましょう。
具体的な使用時期としては7月の1か月に1冊を完成させることが理想的であるといえます。以上が大問［２］の数学ⅡBに対する具体的な対策になります。

大問［３］について

大問［３］は主に数学ⅡBや数学Ⅲからの出題となっています。

• 2017年は空間ベクトル（数学ⅡB）
• 2018年は極限（数学Ⅲ）
• 2019年は数列・場合の数と確率・指数関数と対数関数（数学ⅡB）

大問［３］では、大問［１］や［２］と違って解答の過程を記す記述式による解答が求められます。ここでは、数学ⅡBの記述問題に対する対策について説明していきます。
数学ⅡBの記述問題に対しては「総合的研究-記述式答案の書き方――数学I・A・II・B-」を使って、まず記述式の問題に慣れることから始めましょう。この参考書に含まれている数学ⅠAの範囲に関しては、記述式の解答が求められる可能性が極めて低いため取り組む必要はありません。

「総合的研究-記述式答案の書き方」の使い方！
＜特徴＞
「記述式答案の書き方」のみに限定した数少ない参考書です。そのため、少しの言葉遣いの違いや論理的な説明の順序、条件と命題の違いの意識いろいろな文字の立場の理解など学校の授業などでは深いところまで扱われにくいトピックが丁寧に取り上げられているためこの参考書に取り組むことで減点されにくい答案を書く力を養うことができます。

＜使用時期＞
前出の黄チャートや基礎問題精講などを使って、ある程度の入試基礎レベルの知識やテクニックが身についた状態で取り組み始めることが望ましいです。具体的な使用時期としては、数学ⅡBの基礎問題精講と同じ7月に取り組むことをおすすめします。
以上が大問［３］でよく出題される数学ⅡBの記述問題に対する具体的な対策となります。

大問［４］について

大問［４］ではおもに数学ⅡBや数学Ⅲの範囲から、記述式の解答が求められる問題が出題されることが多くなっています。

• 2017年には微分法（数学Ⅲ）
• 2018年には複素数平面（数学Ⅲ）
• 2019年には2次関数・図形と方程式（数学ⅡB）

ここでは、数学Ⅲに対する対策を説明していきます。まずは、数学ⅠAやⅡBと同じように「チャート式解法と演習数学3（通称：黄チャート）」に取り組み教科書の理解に抜けはないかを確認するとともに、教科書レベルの理解を入試基礎レベルまで底上げしましょう。

「チャート式数学Ⅲ」の使い方！
＜特徴＞
先述したとおりです。数学Ⅲの場合、739題という圧倒的な問題数が大きな特徴です。

＜使用時期＞
具体的な使用時期としては、8月～9月の2か月間をかけて何周も取り組むことで自分の苦手分野を知りましょう。その後、苦手分野を重点的に演習するための準備ができている状態にしておくことが望ましいです。黄チャートで基本的な公式や解法パターンを入試で使えるレベルまで引き上げた後は「合格る計算-数学III-」で数学Ⅲの計算のスピードアップを図りましょう。

青山学院大学理系数学の場合、100分で大問5題に解答しなくてはいけないため、単純計算すると1問にかけられる時間は20分です。しかし、そのうち複雑な計算を含む数学Ⅲがほぼ半分を占めているため「解法は分かっていたのに計算する時間が十分になかった」という事態になりかねません。このような状況を回避するために計算のスピードが必要となります。

「合格る計算-数学Ⅲ-」の使い方！
＜特徴＞
解説が非常に充実していることがこの参考書の大きな特徴の1つで受験生がやりがちな遠回りをすることになる計算方法を的確に提示したうえでそれよりも簡潔に短時間で計算できる方法を説明しています。
年度によって変動する可能性がありますが、マークシート方式で出題される場合、1つのケアレスミスが命取りとなってしまいます。数学Ⅲはパターン問題を理解し暗記するだけで攻略できると言われておりその中で計算方法に関しても暗記すれば正解にたどり着けるものが多く存在します。

前出の解説系参考書や学校の教科書などで土台となる知識を身に着けてからこの参考書を用いて計算方法のパターンも暗記してなるべく短い時間で正確に解答できるようにしましょう。

＜使用時期＞
前述したように、黄チャートなどの解説系参考書や教科書などで土台を固めてから取り組むことをおすすめします。
具体的な使用時期としては10月の１か月間
1周で終わるのではなく何周も取り組むことで、本番でも戦える計算の正確性とスピードを身につけることが理想的です。以上が、大問［４］でよく出題される数学Ⅲの範囲に対する具体的な対策となります。

大問［５］について

大問［５］は例年数学Ⅲの範囲から出題されています。

• 2017年は積分法・極限
• 2018年は積分法
• 2019年は微分法・積分法

これらは全て記述式の解答が求められます。ここでは、まず数学［Ⅲ］の記述式解答が課せられる問題についての具体的な対策に有効な参考書である「大学入試短期集中ゼミノート数学3記述試験対策ノート-2019―書き込み式薄型参考書-」を紹介します。

「大学入試短期集中ゼミノート数学Ⅲ」
＜特徴＞
例題とそれに対する記述解答が左ページに記載されており、右ページで記述のしかたが習得できるようになっています。薄型かつ書き込み式であることも大きな特徴の1つです。頻出かつ重要な45個の項目が厳選されて掲載されています。

＜使用時期＞
前出の「合格る計算」と同時期に取り組むのが望ましいため、ここでは具体的な使用時期を10月とします。数学Ⅲまでの記述力を身につけた後は「青山学院大学理工学部の赤本」に取り組み、本番を意識した実戦演習を行いましょう。

＜特徴＞
実際に青山学院大学の一般入試で出題された問題が3年分掲載されています。合格者の最低点などの入試情報が掲載されていることも大きな特徴の一つです。

＜使用時期＞
今までに紹介した参考書や問題集などで十分な演習を積み、11月ころから入試本番に向けて取り組みはじめるのが理想的です。
ただ、実際には赤本をどの時期にどれぐらいやるべきかは受験生の現在の実力等によって異なります。自分は「いつから・何年分すべきか？」を知りたい方は以下の記事を参考にしてください。
関連：過去問・赤本に関する合格者の使い方・何年分すべきか？

以上が大問［５］の数学Ⅲの記述問題と、全体を網羅する実戦演習に対する具体的な対策となります。

まとめ

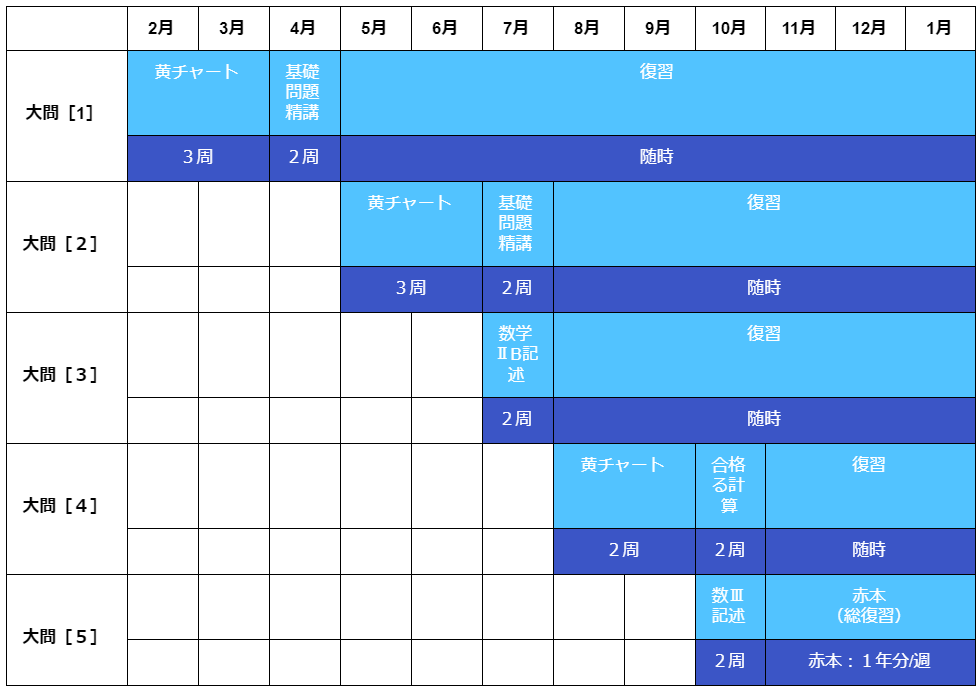
※2月から受験勉強を始めた際の年間スケジュール
大問ごとの傾向と対策について紹介してきましたが、1年間の勉強の流れとしては上記の流れになります。

まず始めるべきは数学Ⅰ・Ⅱ・Ⅲ・A・Bのそれぞれ基本的な問題の解き方パターンや公式のインプットです。いずれも1度で終わらせず、何度も復習するようにしましょう。その後、それぞれの演習系の参考書を用いて何度も繰り返し演習をし、11月以降は赤本の演習に取り組める状態にしましょう。

また、先の参考書で疑問点などが生じた場合は解説を読んで「分かった気」にならず前の講義系の参考書や教科書などに戻って公式などの再理解をすることが大切です。そして、冬にかけて青山学院大学の赤本を用いて時間配分を意識し、より実践的な演習を積むようにしましょう。ぜひ参考にして青山学院大学の数学の目標点である7～8割以上を取れるようにしましょう。

この様に、合格するために重要なことは志望校の特徴にあった勉強を迷いなくすることです！マナビズムでは、自学自習で「何を勉強すればいいのか」「どうやって勉強すればいいのか」を教える「無料受験相談」を実施しています。
「青山学院大学に受かるために何からすればいいか不安！」「受験勉強を始めてみたものの成績が伸びずに不安！」といった人は、ぜひ無料受験相談をお申し込み下さい。