【理系数学編】立教大学の入試対策・オススメ参考書

はじめに

本記事では立教大学の理系数学の傾向と対策、合格するための勉強法について紹介します。立教大学は東京都豊島区西池袋に本部を置く日本の私立大学です。キャンパスは池袋キャンパス （東京都豊島区西池袋）、新座キャンパス （埼玉県新座市北野）の2つで、10学部27学科が設置されており、2万人を超える学生が学ぶマンモス校となっています。首都圏の主な難関私立大学を指すMARCHの『R』の部分を占めている大学です。偏差値としては55.0～67.5で、就職・進路決定率は84.3％(2018年卒)となっています。

立教大学の入試の中で数学Ⅲの範囲を含む理系数学を採用している学部は理学部のみとなっています。数学Ⅲに関しては数学科の個別学部日程方式で必須科目となっています。過去問演習の際はさまざまな入試形式のもの・古い年度のものも使用し、演習慣れをすることをオススメします。この記事では、個別学部日程について説明しています。

概要

• 試験時間：75分または90分
• 配　　点：100点～150点(学科による）
• 目標点　：7～8割
• 問題数　：約25問(数学科/空欄1つを1問と計算)・約20問(物理・化学・生命理学科)
• 形　　式：マークシート方式・記述式
• 構　　成：大問3題または4題

数学科(試験時間90分)
大問［Ⅰ］小問集合
大問［Ⅱ］ 融合問題
大問［Ⅲ］積分
大問［Ⅳ］複素数平面(数学Ⅲ)

物理学・化学・生命理学科(試験時間75分)
大問［Ⅰ］小問集合
大問［Ⅱ］融合問題
大問［Ⅲ］積分

傾向と対策

それでは今から立教大学の理系数学の大問毎の傾向と対策について紹介していきます。

大問［Ⅰ］について

大問［Ⅰ］は小問集合となっています。出題範囲としては数学Ⅰ・A・Ⅱ・Bの内容からまんべんなく出題されます。難易度としては標準的なものが多くなっています。解答形式は全てマークシート式であるため、解答過程を採点者に示すことができません。計算ミスやマークシートのズレなどケアレスミスには日頃の演習の段階から注意するようにしましょう。

学校の授業内容についていけていないと感じる人やまだ学校などで学習していない初学者の人は、まず学校の教科書レベルの知識を理解するために「初めから始める数学」シリーズ（ⅠA・ⅡB、数学科受験者はⅢまで）に取り組みましょう。

　
「初めから始める数学」の使い方！
＜特徴＞
初学者向けの他の参考書と比べても、解説量が多くあることや噛み砕いて丁寧に説明されていることなどから、数学に対して苦手意識を持っている人や高校数学初学者にも分かりやすい参考書となっています。説明文が話し口調で書かれていることなどから親しみやすいという点も大きな特徴の1つです。この参考書は解説に重点を置いた解説書であり問題集ではないため、問題数が十分であるとは言い難いものとなっています。そのため、この参考書で解き方のパターンをインプットした後は(または並行して)他の問題集に取り組むことをおすすめします。

＜使用時期＞
高校数学に関する他の参考書や学校の教科書が授業内容が分からない状態で受験勉強を始めるのであれば、受験勉強開始と同時にこのシリーズの数学Ⅰに取り組み始めましょう。2月から受験勉強を始める場合は、2月に数学Ⅰ、3月に数学Aといったように1か月に1冊を完成させるイメージで進めていけば数学ⅡBまでであれば4か月、数学科志望で数学Ⅲまで取り組むのであれば5か月で終わらせることができます。

学校の教科書や前出の「初めから始める数学」シリーズなどといった、それに準ずるレベルの参考書を使って入試基礎レベルの知識やテクニックをインプットしたあとは「基礎問題精講」シリーズを使って、問題に当たったときにできるだけ早く解法プロセスを思い出すための訓練を行いましょう。数学ⅠA・ⅡB・Ⅲの3冊があります。

　　
「数学 基礎問題精講」の使い方！
＜特徴＞
例題・精講・解答解説・演習問題が見開き1ページに掲載されている、非常に見やすいレイアウトが特徴の参考書となっています。「精講」とはその例題を解く際に必要な公式などが説明されている部分のことです。この部分を深く読み込んで理解することで、他の問題にも応用可能な力を身につけることができます。ただし、演習問題の解説が十分ではないといった欠点があるため、理解が不十分でないと感じた部分に関しては教科書や前出の「初めから始める数学」シリーズなどに戻って、分からないところをそのままにしないようにしましょう。

＜使用時期＞
前述したように解説が十分ではない部分があるため、高校数学に初めて触れる人に対して適した参考書であるとは言い難いものとなっています。そのため、この参考書の中で不明点が出てきた場合は前出の「初めから始める数学」シリーズや学校の参考書などの該当箇所を参考にして、疑問点をそのままにしないようにしましょう。

具体的な使用時期としては5月から7月の3か月で3冊(数学科受験者以外は2冊)を完成させることをおすすめします。
以上が全学科に共通した大問［Ⅰ］の小問集合に対する対策になります。

大問［Ⅱ］について

大問［Ⅱ］は主に数学ⅡBからの出題となっています。1つの分野からの出題ではなく複数分野の融合問題が出題されます。近年では「数列と複素数」「図形と極限」といった範囲が出題されています。解答形式は記述式で問題の難易度は大問Ⅰよりも少し高くなっているため、もし分からない問題に出会った場合でも自分のできる範囲で解答プロセスを記述しておくことをおすすめします。

また試験時間も数学科以外では75分となっているため時間配分にも注意が必要です。頻出分野は「極限」「微分」「積分」「複素数」「図形と計量」「整数」や「確率」となっています。したがって、数学ⅡBの分野別に分かれた試験対策問題集に取り組むのではなく融合問題を演習することが重要です。ここでは、「合格る計算-数学I・A・II・B」をおすすめします。

「合格る計算数学ⅠA・ⅡB」の使い方！
＜特徴＞
インプットした解法パターンを即座に思い出し、できるだけ早く解答に取り掛かったうえで得点につなげるための演習を積むことができる参考書です。各テーマごとに「例題」を通して主に「計算」のコツに重点を置いて丁寧に解説されており、類題演習を通して計算力を定着させることができます。正しい解法・計算法とともにムダの多い、つい受験生がやってしまいがちな方法も紹介されています。比較することで違いがハッキリわかるようになっています。「ここがツボ！」で示されたポイントを「重要ポイントチェック」でスピーディーに確認することができるようになっています。

＜使用時期＞
前出の「基礎問題精講」シリーズで身につけた解法パターンを即座にアウトプットできるようにするために使います。赤本演習に取り掛かる前に、スピーディーに解法を思い出せるようにしておきましょう。具体的な使用時期としては8月と9月の2か月で1冊を完成させることが理想的です。以上が全学科共通の大問［Ⅱ］に対する対策となります。

大問［Ⅲ］について

大問［Ⅲ］も大問［Ⅱ］と同様に数学ⅡBからの出題となっています。大問［Ⅱ］との大きな違いは大問［Ⅱ］が複数分野の融合問題が出題されるのに対して、大問［Ⅲ］では複数分野ではなく1つの分野に絞った出題がされることです。近年は積分の範囲からの出題が多くなっています。解答形式は大問［Ⅱ］と同じ記述式のため、分からない問題に直面してもすぐに諦めることなく自分の分かる範囲で解答を続けることが重要です。しかし時間配分には十分注意しましょう。頻出分野が計算量の多い「微分」と「積分」となっているため、できるだけ多くの問題に触れるための演習をしましょう。微分・積分の分野に特化した参考書として「坂田アキラの数Ⅱの微分積分が面白いほどわかる本」があります。

「坂田アキラの数Ⅱの微分積分が面白いほどわかる本」の使い方！
＜特徴＞
坂田書にはおなじみのキャラクターが存在することや口調が終始一貫されていることなど、読み手に飽きさせないように工夫されています。講義・例題・問題の3つの部分に分かれています。とても丁寧でかみ砕いた解説に定評があり、ただ単に微分積分について解説しているだけではなく微積分の奥深さや面白さなどについても言及している良書となっています。

＜使用時期＞
微分積分のみに特化しているため、微積の分野を得点源としたい人は前出の「合格る計算」シリーズと並行して、苦手意識のある人は10月の1か月で1冊を終えることをおすすめします。
以上が全学科共通の大問［Ⅲ］に対する対策となります。

大問［Ⅳ］について

大問［Ⅳ］は数学科の個別学部日程形式のみで、数学Ⅲの範囲からの出題となっています。2020年度入試では複素数平面が出題されました。基本的に計算量が多い問題が多く出題されるため前出の「合格る計算」シリーズの「合格る計算-数学III-」を使用することをおすすめします。

「合格る計算-数学Ⅲ-」の使い方！
＜特徴＞
解説が非常に充実していることが大きな特徴の1つで、受験生がやりがちな遠回りをすることになる計算方法を的確に提示したうえでそれよりも簡潔に短時間で計算できる方法を説明しています。数学Ⅲはパターン問題を理解し暗記するだけで攻略できると言われており、その中で計算方法に関しても暗記すれば正解にたどり着けるものが多く存在します。前出の解説系参考書や学校の教科書などで土台となる知識を身に着けてから、この参考書を用いて計算方法のパターンを暗記してなるべく短い時間で正確に解答できるようにしましょう。

＜使用時期＞
前述したように、解説系参考書や教科書などで土台を固めてから取り組むことをおすすめします。具体的な使用時期としては数学科受験者は大問［Ⅲ］の対策と並行して(10月まで)、本番でも戦える計算の正確性とスピードを身につけることが理想的です。以上が数学科のみの大問［Ⅳ］の数学Ⅲの範囲に対する対策となります。

数学Ⅲ(数学科以外は数学ⅡB)までの解答力を身につけた後は「立教大学理学部個別学部日程」の赤本に取り組み、本番を意識した実戦演習を行いましょう。

＜特徴＞
実際に立教大学の一般入試で出題された問題が3年分掲載されています。合格者の最低点などの入試情報が掲載されていることも大きな特徴の一つです。

＜使用時期＞
今までに紹介した参考書や問題集などで十分な演習を積み、11月ころから入試本番に向けて取り組みはじめるのが理想的です。
ただ、実際には赤本をどの時期にどれぐらいやるべきかは受験生の現在の実力等によって異なります。自分は「いつから・何年分すべきか？」を知りたい方は以下の記事を参考にしてください。
過去問・赤本に関する合格者の使い方・何年分すべきか？

まとめ

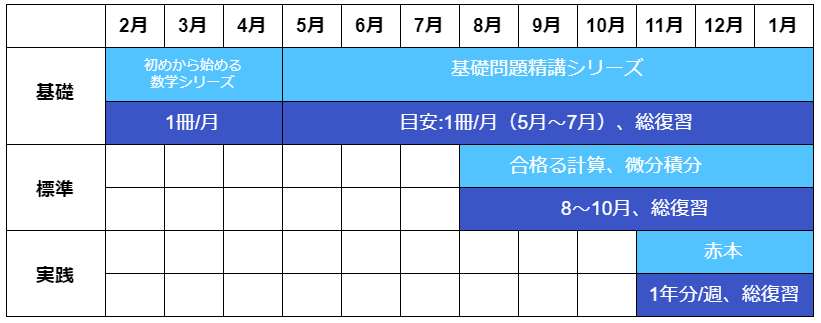
※2月から受験勉強を始めた際の年間スケジュール

大問ごとの傾向と対策について紹介してきましたが、1年間の勉強の流れとしては上記の流れになります。
まず始めるべきは数学Ⅰ・Ⅱ・A・B(数学科はⅢ)の基本的な問題の解き方のパターンのインプットです。教科書やそれに準ずる参考書を用いて,理解に穴を作らないようにしましょう。いずれも1度で終わらせず、何度も復習することが最も大切です。その後、それぞれの演習系の参考書を用いて何度も実戦演習をし、秋以降はスムーズに赤本の演習に取り組んでいけるようにしましょう。

また、先の参考書で疑問点などが生じた場合は解説を読んで「分かった気」になるのではなく、前のレベルの講義系参考書や教科書などに戻って公式などの再理解をすることも大切です。そして、冬にかけて立教大学の赤本を用いて時間配分などを意識しながらより実践的な演習を積むようにしましょう。ぜひ参考にして立教大学の数学の目標点である7割～8割以上を取れるようにしましょう。