【数学編】勉強法・オススメ参考書・問題集

数学勉強法

まず、数学勉強法について紹介する前に数学という科目の性質について理解しておきましょう。

数学の科目の性質

数学とは「どうしてその問題が解けなかったか、どういった視点・考え方が足りなかったか」ということを常に分析し続けなければならない教科です。
これは数学に限った話ではないですが、数学では特に意識すべきことになります。というのも、数学という科目は、難問とされる問題でも「解答を見ればわかる」というものが多いからです。

しかし、解答を見て「なるほど、そういうことか」と分かるのと、試験会場で実際にその問題を解けることとは大きな差があります。
その格差を埋めるために、先ほど説明したような分析を最初の段階から行う必要があります。どの段階においても大事なのは、一問一問、とことん理解しながら進むこと。これを他教科以上に求められる科目となります。

数学の学習手順

1. 教科書レベルの理解と暗記
2. パターンの暗記
3. アウトプット

1段階は「教科書の例題がすべて解ける」のが1段階目の目標になります。
2段階で丸暗記数学にならないようにするのが、この1段階目の役割です。
しっかりと土台を固める（理解する）ことで、今後の数学が決まると言っても過言ではないでしょう。

2段階は、パターンの暗記です。
すなわちパターン問題と呼ばれる品種問題を問題と解法セットで暗記しましょう。ただ、丸暗記ではなく、「なぜその解法が使えるのか」という観点を忘れずにしましょう。ここで理解を助けるのが1段階であり、1段階がおろそかだと、丸暗記になります。

3段階は、アウトプットです。
ここまで身につけてきた武器を使いこなすためには、やはり「量」が非常に大事です。
解けない問題に出くわしたときこそ財産です。「なぜ解けなかったのか」を追求して、数学力を高めましょう。

勉強の基本は「インプット→アウトプット」の流れで勉強することです。このように数学においても例外ではありません。
では、数学の「インプット」とは何でしょう？「公式を覚える」これが頭に浮かびましたか？たいていの人はそうでしょう。
もちろん、それは間違ったことではありませんし、「公式」も覚えなければならない大事な要素の１つです。しかし、「公式」を覚えておけば、大学入試問題が解けるでしょうか？

定期試験なら何とかなるかも知れませんが、大学入試問題は「公式」だけ覚えていたところで全く手が出ないはずです。そもそも、それで何とかなっていないから、今こうして数学で悩んでいるのではありませんか？つまり、「公式」を覚えておくだけでは、数学のインプットに対する勉強としては不十分だということです。

では一体どうすればいいのでしょう？
それは「解き方を覚えてしまう」です。
大学入試には頻出の出題パターンというものがあります。多くの問題はその枠から外れることはありません。ですから、「このタイプの問題は、この公式を使って、こうしてああして…それで答えを出す！」という様に、問題の解き始めから解答が出るまでのプロセスを完璧に理解し覚えてしまうのです。

そのプロセスのことを「解法パターン」といいます。
「解法パターン」は単語の意味を丸暗記するように暗記したのでは意味がありません。必ず、「なぜこういう解き方になるのか」を理解したうえで、暗記することが重要です。これを「理解型暗記」といいます。

そして、その「解法パターン」を関関同立合格に必要な量だけ全て覚えてしまえばいいのです。お分かりいただけたでしょうか？数学は暗記科目なのです。今まで「自分にはセンスがないから数学は無理」だと思っていた人、まだ諦めるのは早いです。関関同立レベルの入試問題にセンスなど必要ありません。
この「理解型暗記」の数学なら今までと違った、全く新しい数学の世界が見えてきます。

それでは上記の｢解法パターンの暗記｣のために使用すべきオススメ参考書を紹介します。

アウトプットの勉強に入る最適な時期は？

インプットの勉強法では、数学は理解型暗記の科目であり、受験初期はまず解法パターンを定着させなければならない、という話をしましたね？
ただし、それだけで合格レベルまでの完成度になるわけではありません。ここからは、いよいよアウトプットの勉強に入っていきます。

アウトプットとは、要は演習のことです。
センター試験の過去問・演習系の問題集・赤本などを使って少しずつレベルを上げていきながら、最終的に志望校の入試レベルの問題が解けるようになればいいのです。

そもそも多くの受験生がここで失敗してしまっているのですが、「数学は解くものだ！」という意識が強すぎて、受験初期からアウトプットの勉強をしてしまっているのです。
アウトプットで大事なことは、インプットした「解法パターン」を「使いこなす」練習をしているという意識を持つことです。

決して未知の問題にチャレンジしているわけではありません。インプットの学習が完成しているなら、すでにやったことのある知識の中から解くことができるはずなのです。
この「覚えたことを出す」というイメージが大切です。 

アウトプット初期の勉強法

そこで、あなたがどこの大学を志望していたとしても、数学のアウトプットの初期段階は、センター試験レベルの問題が解けるようになることです。
センター試験は基本的に奇問・難問の類が出題されることはありません。

あなたがインプットの勉強をしっかりとこなしていれば、その時点で、６割～７割(120点～140点)ほどの点数が取れるはずです。
しかし、それ以上の点数が取れない。それはなぜか？それは「理解して→覚えて→出す」の3つ目「出す」の練習をしていないからです。
この「出す」というのがいわゆるアウトプットの勉強なわけですが、そこでセンター試験という典型的な基本レベルの問題を利用することで、「出す」ということに慣れるわけです。

目標は、志望校や志望学部にもよりますが、８割(160点)程度の点数をとることです。
この点数を１つの目安にしてください。
なぜなら、センターで８割取れる状態で、私大・２次の演習に移ると非常にスムーズに学習が展開するからです。

私大・２次レベルの演習参考書は、ある程度「この程度のことは知っていて当たりまえ」という設定で解説が進んでいきます。ですから、理解が乏しいと全く理解できないということがおき、これがいわゆる「挫折」の原因です。必ずこの流れを大切にしてください。

アウトプット後期の勉強法

私大・２次レベルの問題は一気に難易度が上がります。最初は少し苦しいと思いますが、グッとこらえてください。
私大・２次レベルの演習に入ったあと、イメージとして持っておいてほしい考え方があります。それは、「アウトプットだけど、一歩上の解法パターンをインプットする」というイメージです。

難易度の高い問題は、難易度の高い問題なりにパターンに落とし込むことがやはりできます。最初は知らないことですから、できなくて当たり前。一向に構いません。こらえてください。多くの受験生が「数学の勉強と言えばコレ！」だと思っている、いわゆる「初見の問題にできるだけ多く触れておく演習」というのは受験の最後の最後です。

アウトプット時の注意点

このアウトプットの時期に到達したあとに使用する参考書の選び方や使用する順番を間違えると全く成績が伸びないということが起こり得る恐ろしい段階です。ここを間違えると間違いなく受かりません。あなたにはあなたにあった合格のルートがあります。それでは、関関同立合格のために必要なアウトプット系参考書を、使用すべき順番で紹介していきます。

数学オススメ参考書・問題集

それでは、「解法パターン暗記」が重要だと分かった上で、解法パターン暗記をするためにおすすめの参考書について紹介します！

　
「やさしい高校数学」の使い方はコチラ！
＜特徴＞
この参考書の何よりの特徴は、キャラクターの掛け合いを通して高校数学の内容を理解することができる、まさに「やさしい」参考書である点です。数学の初学者や苦手意識のある人でも楽しく数学の土台を作っていくことができます。

またイラストや図が豊富に使用されているの豊富に使われているので直感的な理解が容易になっている他、数式や関数、ベクトルを図形的に捉える力をつけることもできます。

＜使用時期＞
入試初期（ⅠA・ⅡB）入試中期（Ⅲ）
目標進度：1周/週（ⅠA）1周/2週（ⅡB）
目標習熟期間：1~2ヶ月（ⅠA）1~2ヶ月（ⅡB）

「重要事項完全習得編」の使い方はコチラ！
＜特徴＞
本書は「受験頻出のパターン」が一通り網羅されているので、この1冊を完璧にし、受験数学に必要なインプットの基礎を完成させましょう。
数学ⅠＡⅡＢの範囲で152題の例題が掲載されています。例題数は、基礎的なインプット完成のために必要最小限の量となっており、これから受験数学を勉強する上で軸となる参考書です。関関同立受験で、数学を使用するならば、文系・理系問わず初めにこなすべき問題集です。

＜使用時期＞
入試初期
目標進度：40題/週
目標習熟期間：2~3ヶ月

「数学Ⅲ 基礎問題精講」の使い方はコチラ！
＜特徴＞
この参考書は「基礎はできても、応用になると全く歯が立たない…」「教科書の問題は出来るけど、実践系の問題は苦手…」と感じている人におすすめの問題集となっています。
問題レベルは教科書の章末問題～入試基礎レベルです。この参考書に取り組むことで、教科書レベルと入試問題の架け橋となることが期待できるでしょう。

＜使用時期＞
入試中期
目標進度：1章/週
目標習熟期間：2~3ヶ月

「数学重要問題集」
＜特徴＞
国公立大二次試験や私立大試験のうち、主に理系学部の良問を精選して収録。入試の基本~標準レベルを「A問題」、入試の標準~やや難レベルを「B問題」、入試の発展レベルを「C問題」として収録しています。難関大学志望であればA・B問題を解けるようにしましょう。

＜使用時期＞
入試中期～入試後期
目標進度：1周/1~2月
目標習熟期間：2~3ヶ月

「合格る計算-数学Ⅲ-」の使い方はコチラ！
＜特徴＞
「合格る計算」は、制限時間がある入試で使える計算のテクニックを無駄なく習得することができる参考書となっています。インプットした解法パターンを即座に思い出し、得点につなげるための演習を積むことができます。

＜使用時期＞
基礎問題精講Ⅲ修了後～入試本番
目標進度：1周/1~2週
目標習熟期間：2~3ヶ月

「微積分/基礎の極意」
＜特徴＞
1章に計算問題集、2章は微積分の得する知識集、3章はパターン問題難問を収録しています。特に面白いのが2章です。こちらで得た知識があるかないかで入試問題に対する見方が変わります。式を見ただけでグラフが描けたり、極限計算が一瞬で片付くことなどお宝レベルの知識が山盛りです。

＜使用時期＞
入試中期～入試本番
目標進度：1章/週
目標習熟期間1~2ヶ月
以上が数学のオススメ参考書・問題集になります。

まとめ

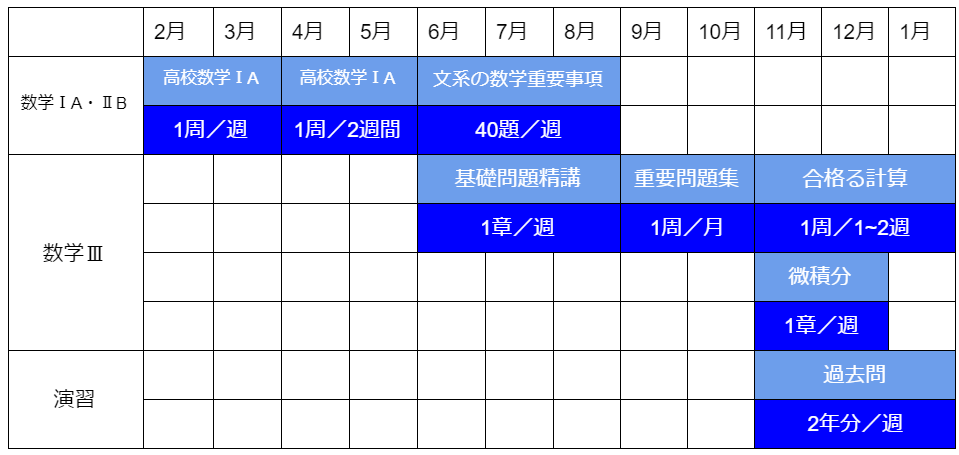
1年間の学習スケジュールはこの様になります。
※2月から受験勉強をスタートした場合

冒頭で触れたとおり、数学を得意科目にするためには「どうしてその問題が解けなかったか、どういった視点・考え方が足りなかったか」ということを常に分析し続けなければならない教科です。

1. 教科書レベルの理解と暗記
2. パターンの暗記
3. アウトプット

この様な勉強の流れと目的意識を持った上で受験勉強を始めましょう。